How To Solve Angle Relationships

Bending RELATIONSHIPS

2 or more angles can be related, if sure conditions are met. Hither, we will learn different types of bending relationships.

(i) Congruent Angles

(ii) Vertical Angles

(iii) Complementary Angles

(4) Supplementary Angles

(v) Side by side Angles

(vi) Side by side Angles in Parallelogram

(vii) Linear Pair

(viii) Corresponding Angles

(ix) Alternate Interior Angles

(x) Alternate Exterior Angles

(xi) Sequent Interior Angles

(xii) Consecutive Outside Angles

Allow the states see the above dissimilar types of bending relationships in detail.

(i) Congruent Angles :

Congruent angles are angles that take the same measure.

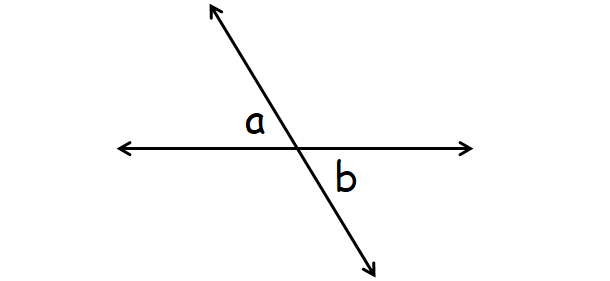
(ii) Vertical Angles :

Vertical angles take a mutual vertex, but they are never adjacentangles. And also,vertical angles are e'er congruent.

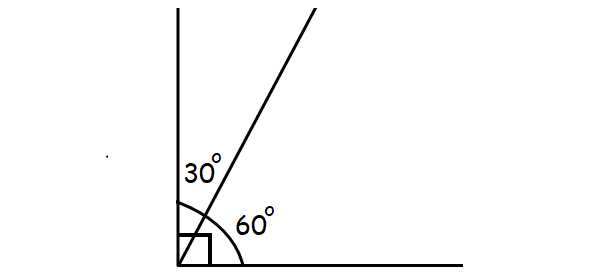
(iii) Complementary Angles :

If the sum of two angles is 90⁰, then those two angles are called as complementary angles.

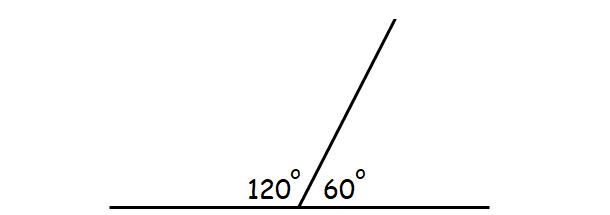
(iv) Supplementary Angles :

If the sum of two angles is 180 ° , and so those two angles are called equally supplementary angles.

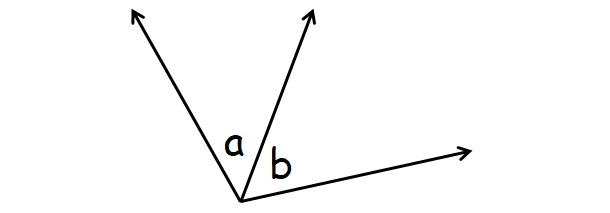
(five) Side by side Angles :

Side by side angles are two angles that have a common vertex and a common side.

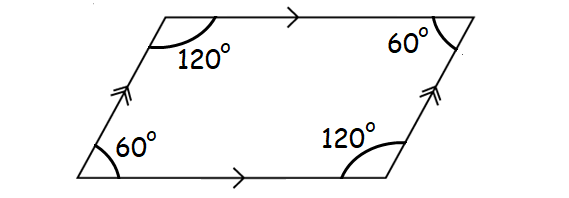
(half dozen) Consecutive Angles in Parallelogram :

Any 2 consecutive angles of a parallelogram are supplementary.

(vii) Linear Pair :

A linear pair is a pair of adjacent angles formed when ii lines intersect.

The 2 angles of a linear pair are always supplementary , which means their measures add up to 180°.

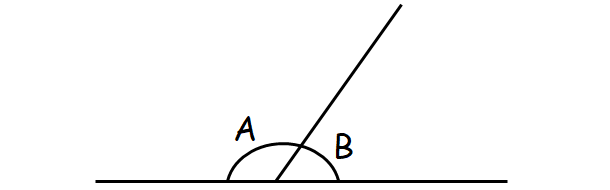
In the figure above A and B are linear pair.

A + B = 180 °

To know nigh Corresponding Angles, Alternate Interior Angles, Alternating Exterior Angles, Sequent Interior Angles and Consecutive Outside Angles in item,

please click here

Solved Questions

Questions 1-vii : Discover the value of 10 in the diagram.

Question 1 :

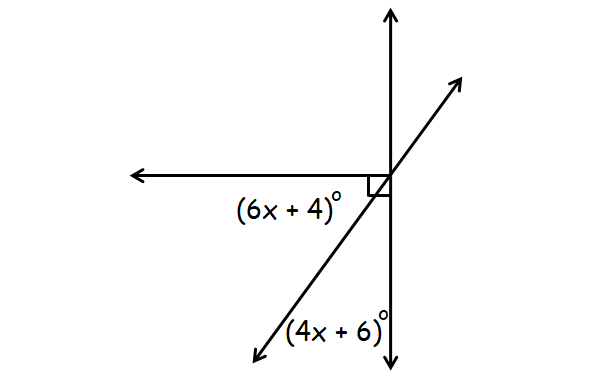
Answer :

In the diagram above, (6x + 4)° and (4x + 6)° are complementary.

(6x + iv)° + (4x + vi)° = 90°

6x + four + 4x + 6 = xc

10x + 10 = 90

10x = 80

x = 8

Question 2 :

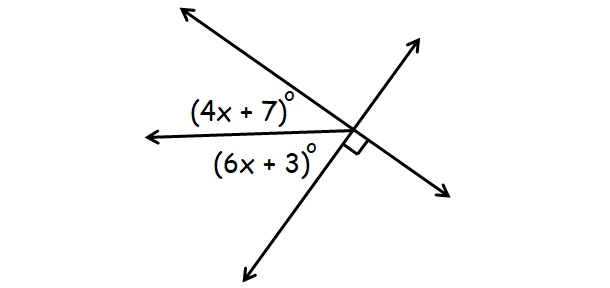
Answer :

In the diagram above, (4x + seven)° and (6x + 3)° are complementary.

(4x + 7)° + (6x + 3)° = 90°

4x + vii + 6x + 3 = 90

10x + x = 90

10x = 80

x = 8

Question 3 :

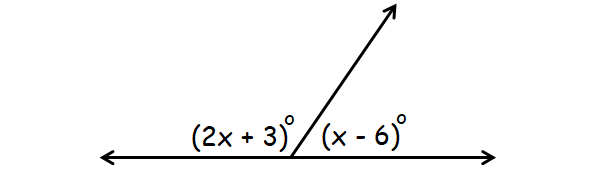
Respond :

In the diagram above, (2x + 3)° and (x - 6)° are supplementary angles.

(2x + 3)° + (10 - 6)° = 180°

2x + 3 + x - half-dozen = 180

3x - 3 = 180

3x = 183

x = 61

Question iv :

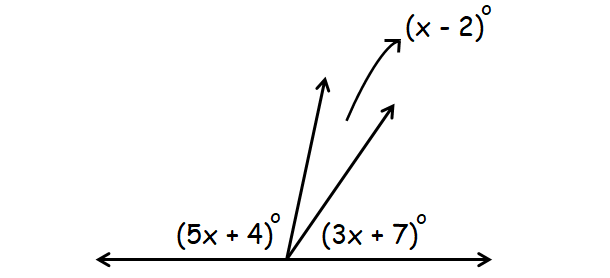
Respond :

In the diagram above, (5x + iv)°, (10 - 2)° and (3x + 7)° are supplementary angles.

(5x + four)° + (x - two)° + (3x + 7)° = 180°

5x + 4 + x -2 + 3x + 7 = 180

9x + 9 = 180

9x = 171

10 = 19

Question 5 :

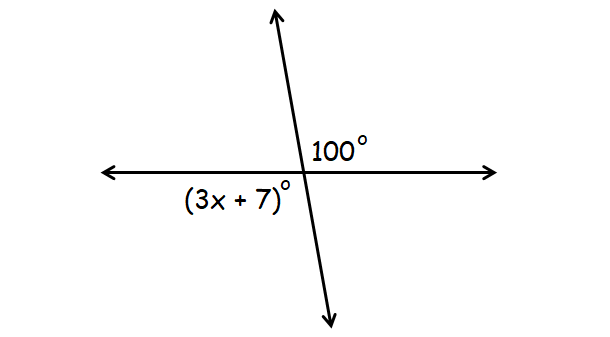
Answer :

In the diagram above, (3x + 7)° and 100° are vertical angles.

(3x + 7)° = 100°

3x + 7 = 100

3x = 93

10 = 31

Question half dozen :

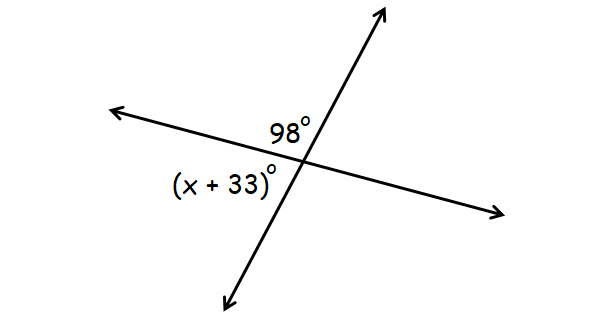
Respond :

In the diagram above, (10 + 33)° and 98° form a linear pair.

(ten + 33)° + 98° = 180°

x + 33 + 98 = 180

ten + 131 = 180

ten = 49

Question vii :

In the diagram given beneath, l_ilines 50_ii are parallel and t is a transversal. Find the value of x.

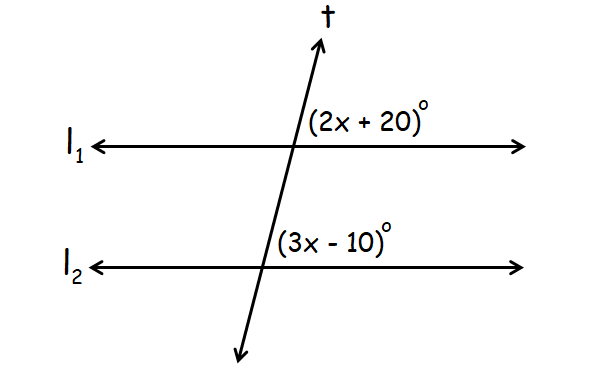
Answer :

In the above diagram, (2x + 20) ° and (3x - 10) ° are respective angles.

When 2 parallel lines are cut by a transversal, corresponding angles are coinciding.

(2x + twenty)° = (3x - 10)°

2x + twenty = 3x - ten

30 = x

Question eight :

In the diagram given below, l₁lines 50_two are parallel and t is a transversal. Detect the value of x.

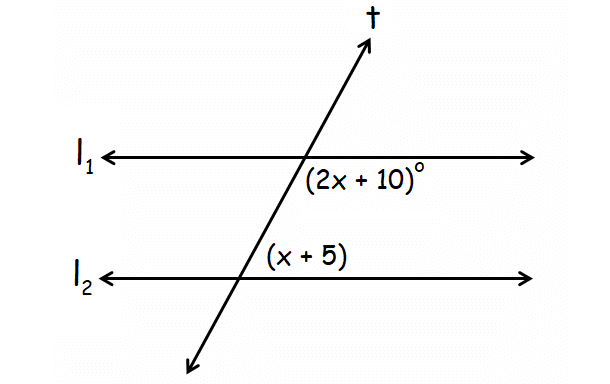
Answer :

In the above diagram, (2x + x)° and (x + 5)° are sequent interior angles.

When 2 parallel lines are cutting by a transversal, consecutive interior angles are supplementary.

(2x + 10)° + (x + 5)° = 180 °

2x + 10 + x + 5 = 180

3x + 15 = 180

3x = 165

ten = 55

Question 9 :

In the diagram given below, lines a and b are parallel and t is a transversal. Notice the value of ten.

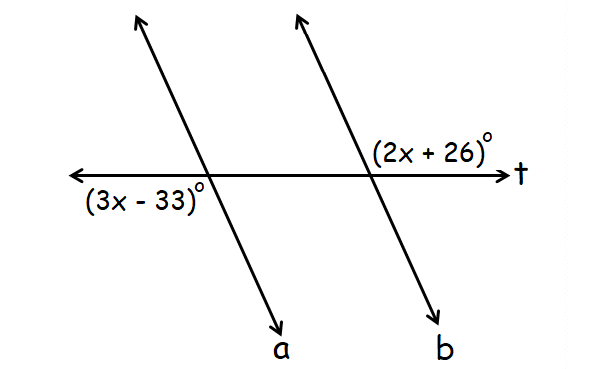
Answer :

In the diagram diagram, (2x + 26)° and (3x - 33)° are alternate interior angles.

When 2 parallel lines are cut past a transversal, alternate interior angles are congruent.

(2x + 26)° = (3x - 33) °

2x + 26 = 3x - 33

59 = x

Question 10 :

In the diagram shown beneath, f ind the value of x.

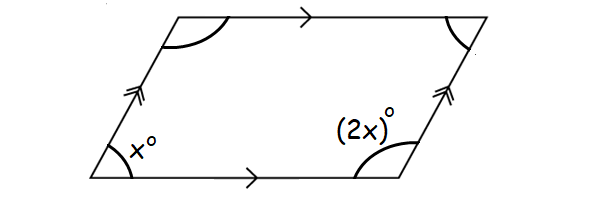
Respond :

In the diagram diagram, it is articulate that AB||CD and Advertizement||BC.

So ABCD is a parallelogram.

In a parallelogram, two consecutive angles are always supplementary.

10° + (2x)° = 180 °

ten + 2x = 180

3x = 180

x = lx

Kindly mail your feedback tov4formath@gmail.com

We e'er appreciate your feedback.