Differential Equation Spring Mass System
17.3: Applications of 2d-Social club Differential Equations
- Folio ID
- 2628
- Solve a 2d-order differential equation representing simple harmonic motion.
- Solve a 2nd-guild differential equation representing damped simple harmonic move.
- Solve a second-order differential equation representing forced simple harmonic move.
- Solve a 2d-gild differential equation representing accuse and current in an RLC series excursion.
We saw in the chapter introduction that second-order linear differential equations are used to model many situations in physics and engineering. In this section, we expect at how this works for systems of an object with mass attached to a vertical leap and an electric circuit containing a resistor, an inductor, and a capacitor connected in series. Models such as these can be used to estimate other more complicated situations; for example, bonds between atoms or molecules are oftentimes modeled every bit springs that vibrate, as described by these same differential equations.
Simple Harmonic Motion
Consider a mass suspended from a jump attached to a rigid back up. (This is commonly called a spring-mass system.) Gravity is pulling the mass downwardly and the restoring forcefulness of the spring is pulling the mass upward. Equally shown in Effigy \(\PageIndex{1}\), when these 2 forces are equal, the mass is said to be at the equilibrium position. If the mass is displaced from equilibrium, it oscillates upwardly and downwards. This beliefs tin can be modeled by a second-order abiding-coefficient differential equation.
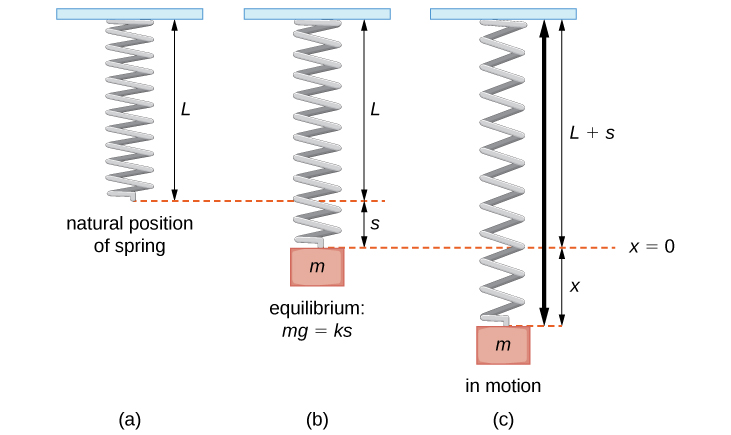
Let \(x(t)\) denote the deportation of the mass from equilibrium. Note that for bound-mass systems of this type, it is customary to adopt the convention that downward is positive. Thus, a positive displacement indicates the mass is beneath the equilibrium signal, whereas a negative displacement indicates the mass is above equilibrium. Deportation is normally given in feet in the English system or meters in the metric system.
Consider the forces acting on the mass. The forcefulness of gravity is given by mg.mg. In the English organization, mass is in slugs and the dispatch resulting from gravity is in feet per second squared. The acceleration resulting from gravity is constant, so in the English language organisation, \(grand=32\, ft/sec^2\). Recall that one slug-pes/sectwo is a pound, so the expression mg tin can be expressed in pounds. Metric organisation units are kilograms for mass and 1000/sectwo for gravitational acceleration. In the metric system, nosotros have \(g=nine.8\) m/sec2.
Co-ordinate to Hooke'south police, the restoring force of the spring is proportional to the displacement and acts in the opposite management from the displacement, and so the restoring force is given by \(−k(due south+x).\) The spring constant is given in pounds per foot in the English organisation and in newtons per meter in the metric system.
Now, by Newton's second law, the sum of the forces on the system (gravity plus the restoring force) is equal to mass times acceleration, so we take
\[\begin{align*}mx″ &=−k(s+x)+mg \\[4pt] &=−ks−kx+mg. \end{marshal*}\]
Even so, by the way nosotros have defined our equilibrium position, \(mg=ks\), the differential equation becomes
\[mx″+kx=0. \nonumber \]
Information technology is convenient to rearrange this equation and introduce a new variable, called the angular frequency, \(ω\). Letting \(ω=\sqrt{chiliad/m}\), nosotros can write the equation as
\[x''+ω^2x=0. \nonumber \]
This differential equation has the general solution
\[x(t)=c_1 \cos ωt+c_2 \sin ωt, \label{GeneralSol} \]
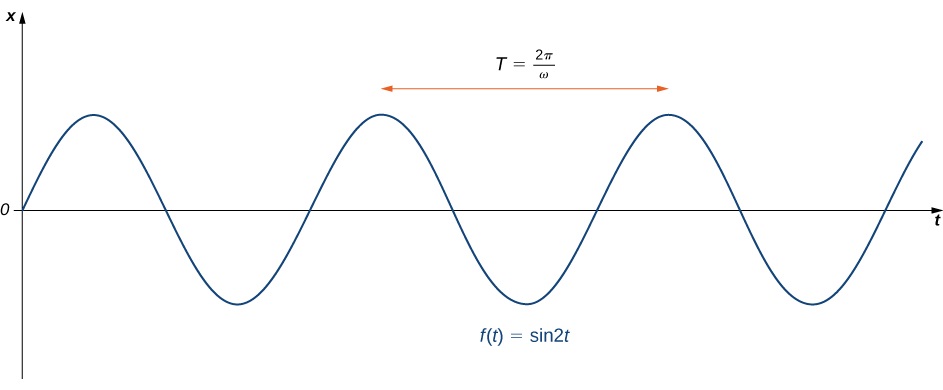
which gives the position of the mass at any indicate in time. The motility of the mass is called simple harmonic motion. The period of this motion (the time it takes to complete ane oscillation) is \(T=\dfrac{2π}{ω}\) and the frequency is \(f=\dfrac{1}{T}=\dfrac{ω}{2π}\) (Figure \(\PageIndex{2}\)).
Presume an object weighing ii lb stretches a spring 6 in. Find the equation of move if the leap is released from the equilibrium position with an upward velocity of 16 ft/sec. What is the catamenia of the move?
Solution
Nosotros first need to observe the spring constant. Nosotros have
\[\begin{align*}mg &=ks\\[4pt] ii &=chiliad \left(\dfrac{1}{two}\correct)\\[4pt] k &=four. \end{marshal*}\]
We also know that weight \(W\) equals the production of mass \(chiliad\) and the acceleration due to gravity \(g\). In English units, the acceleration due to gravity is 32 ft/sec2.
\[\brainstorm{align*}W &=mg\\[4pt] 2 &=m(32)\\[4pt] m &=\dfrac{1}{16}\cease{align*}\]
Thus, the differential equation representing this system is
\[\dfrac{1}{16}x″+4x=0. \nonumber \]
Multiplying through by 16, we get \(x''+64x=0,\) which can also exist written in the grade \(x''+(8^2)x=0.\) This equation has the general solution
\[x(t)=c_1 \cos (8t)+c_2 \sin (8t). \nonumber \]
The mass was released from the equilibrium position, so \(x(0)=0\), and it had an initial upwardly velocity of 16 ft/sec, so \(x′(0)=−16\). Applying these initial weather to solve for \(c_1\) and \(c_2\). gives
\[x(t)=−2 \sin 8t. \nonumber \]
The menstruum of this motion is \(\dfrac{2π}{8}=\dfrac{π}{4}\) sec.
A 200-g mass stretches a spring 5 cm. Find the equation of move of the mass if information technology is released from residuum from a position 10 cm beneath the equilibrium position. What is the frequency of this move?
- Hint
-
Starting time notice the spring constant.
- Answer
-
\(x(t)=0.ane \cos (14t)\) (in meters); frequency is \(\dfrac{14}{2π}\) Hz.
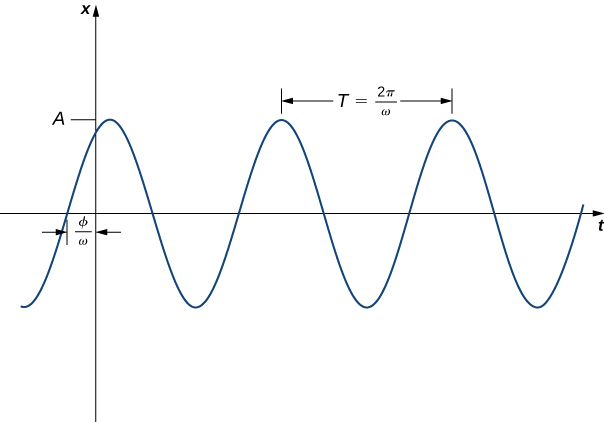
Writing the general solution in the form \(10(t)=c_1 \cos (ωt)+c_2 \sin(ωt)\) (Equation \ref{GeneralSol}) has some advantages. It is easy to see the link between the differential equation and the solution, and the period and frequency of move are evident. This grade of the function tells us very little about the aamplitude of the motion, however. In some situations, nosotros may adopt to write the solution in the course
\[ten(t)=A \sin (ωt+ϕ). \nonumber \]
Although the link to the differential equation is not as explicit in this case, the period and frequency of movement are still evident. Furthermore, the aamplitude of the motion, \(A,\) is obvious in this class of the function. The constant \(ϕ\) is chosen a phase shift and has the effect of shifting the graph of the function to the left or right.
To convert the solution to this form, nosotros desire to find the values of \(A\) and \(ϕ\) such that
\[c_1 \cos (ωt)+c_2 \sin (ωt)=A \sin (ωt+ϕ). \nonumber \]
We first apply the trigonometric identity
\[\sin (α+β)= \sin α \cos β+ \cos α \sin β \nonumber \]
to get
\[\begin{align*} c_1 \cos (ωt)+c_2 \sin (ωt) &= A( \sin (ωt) \cos ϕ+ \cos (ωt) \sin ϕ) \\[4pt] &= A \sin ϕ( \cos (ωt))+A \cos ϕ( \sin (ωt)). \finish{marshal*}\]
Thus,
\[c1=A \sin ϕ \text{ and } c_2=A \cos ϕ. \nonumber \]
If we foursquare both of these equations and add them together, nosotros become
\[\brainstorm{align*}c_1^2+c_2^2 &=A^2 \sin _2 ϕ+A^2 \cos _2 ϕ \\[4pt] &=A^ii( \sin ^2 ϕ+ \cos ^two ϕ) \\[4pt] &=A^2. \end{marshal*}\]
Thus,
\[A=\sqrt{c_1^two+c_2^two}. \nonumber \]
Now, to find \(ϕ\), go back to the equations for \(c_1\) and \(c_2\), but this time, divide the starting time equation by the second equation to go
\[\brainstorm{marshal*} \dfrac{c_1}{c_2} &=\dfrac{A \sin ϕ}{A \cos ϕ} \\[4pt] &= \tan ϕ. \end{marshal*} \nonumber \]
Then,
\[\tan ϕ= \dfrac{c_1}{c_2}. \nonumber \]
We summarize this finding in the following theorem.
The function \(ten(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\) can be written in the form \(x(t)=A \sin (ωt+ϕ)\), where \(A=\sqrt{c_1^2+c_2^ii}\) and \( \tan ϕ = \dfrac{c_1}{c_2}\).
Note that when using the formula \( \tan ϕ=\dfrac{c_1}{c_2}\) to notice \(ϕ\), we must accept intendance to ensure \(ϕ\) is in the right quadrant (Figure \(\PageIndex{3}\)).
Express the following functions in the form \(A \sin (ωt+ϕ) \). What is the frequency of motion? The amplitude?
- \(x(t)=2 \cos (3t)+ \sin (3t)\)
- \(x(t)=3 \cos (2t)−2 \sin (2t)\)
Solution
We have
\[A=\sqrt{c_1^2+c_2^2}=\sqrt{2^2+1^2}=\sqrt{five} \nonumber \]
and
\[ \tan ϕ = \dfrac{c_1}{c_2}=\dfrac{2}{1}=2. \nonumber \]
Notation that both \(c_1\) and \(c_2\) are positive, so \(ϕ\) is in the first quadrant. Thus,
\[ϕ≈ane.107 \; \text{rad}, \nonumber \]
and so we have
\[ ten(t) = 2 \cos (3t)+ \sin (3t) =5 \sin (3t+1.107). \nonumber \]
The frequency is \(\dfrac{ω}{2π}=\dfrac{3}{2π}≈0.477.\) The amplitude is \(\sqrt{5}\).
- Nosotros have
\[A=\sqrt{c_1^ii+c_2^ii}=\sqrt{three^2+2^ii}=\sqrt{xiii} \nonumber \]
and\[ \tan ϕ = \dfrac{c_1}{c_2}= \dfrac{3}{−2}=−\dfrac{three}{ii}. \nonumber \]
Note that \(c_1\) is positive but \(c_2\) is negative, so \(ϕ\) is in the quaternary quadrant. Thus,\[ϕ≈−0.983 \; \text{rad}, \nonumber \]
then we have\[\begin{align*} x(t) &=3 \cos (2t) −2 \sin (2t) \\ &= \sqrt{thirteen} \sin (2t−0.983). \cease{align*}\]
The frequency is \(\dfrac{ω}{2π}=\dfrac{2}{2π}≈0.318.\) The amplitude is \(\sqrt{13}\).
Express the function \(x(t)= \cos (4t) + 4 \sin (4t)\) in the form \(A \sin (ωt+ϕ) \). What is the frequency of move? The aamplitude?
- Hint
-
Apply the process from the Case \(\PageIndex{2}\).
- Answer
-
\(x(t)= \sqrt{17} \sin (4t+0.245), \text{frequency} =\dfrac{four}{2π}≈0.637, A=\sqrt{17}\)
Damped Vibrations
With the model just described, the motility of the mass continues indefinitely. Clearly, this doesn't happen in the real world. In the existent world, there is almost always some friction in the organization, which causes the oscillations to dice off slowly—an result chosen damping. So now let'south wait at how to incorporate that damping strength into our differential equation.
Physical leap-mass systems almost e'er have some damping every bit a event of friction, air resistance, or a physical damper, chosen a dashpot (a pneumatic cylinder; Figure \(\PageIndex{four}\)).
Considering damping is primarily a friction strength, we assume it is proportional to the velocity of the mass and acts in the opposite direction. So the damping force is given by \(−bx′\) for some abiding \(b>0\). Over again applying Newton's second law, the differential equation becomes
\[mx″+bx′+kx=0. \nonumber \]
Then the associated feature equation is
\[mλ^2+bλ+1000=0. \nonumber \]
Applying the quadratic formula, we accept
\[λ=\dfrac{−b±\sqrt{b^2−4mk}}{2m}. \nonumber \]
Just as in Second-Order Linear Equations we consider 3 cases, based on whether the feature equation has distinct real roots, a repeated real root, or circuitous conjugate roots.
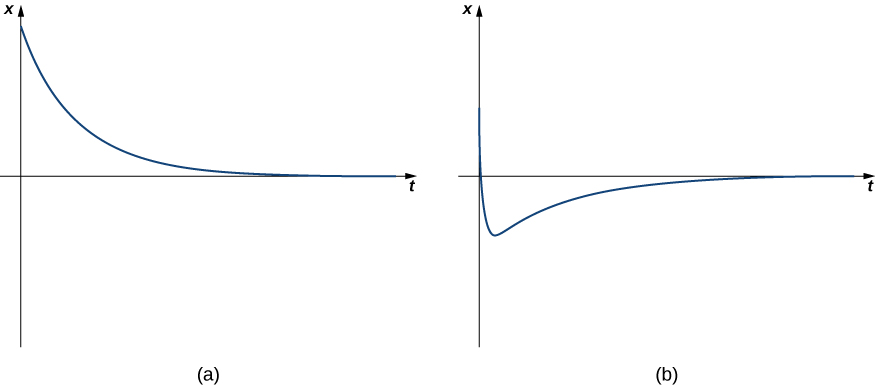
Case i: Overdamped Vibrations
When \(b^2>4mk\), nosotros say the system is overdamped . The general solution has the form
\[x(t)=c_1e^{λ_1t}+c_2e^{λ_2t}, \nonumber \]
where both \(λ_1\) and \(λ_2\) are less than null. Considering the exponents are negative, the deportation decays to zero over time, usually quite quickly. Overdamped systems exercise not oscillate (no more than 1 change of direction), only simply motion back toward the equilibrium position. Figure \(\PageIndex{five}\) shows what typical critically damped behavior looks similar.
A sixteen-lb mass is attached to a 10-ft spring. When the mass comes to rest in the equilibrium position, the jump measures 15 ft 4 in. The organisation is immersed in a medium that imparts a damping force equal to 5252 times the instantaneous velocity of the mass. Find the equation of motility if the mass is pushed upwardly from the equilibrium position with an initial upward velocity of 5 ft/sec. What is the position of the mass afterwards x sec? Its velocity?
Solution
The mass stretches the spring 5 ft iv in., or \(\dfrac{16}{3}\) ft. Thus, \(16=\left(\dfrac{16}{3}\right)1000,\) so \(yard=3.\) We also have \(1000=\dfrac{16}{32}=\dfrac{1}{2}\), so the differential equation is
\[\dfrac{5}{2}x′+3x=0. \nonumber \]
Multiplying through past ii gives \(ten″+5x′+6x=0\), which has the full general solution
\[ten(t)=c_1e^{−2t}+c_2e^{−3t}. \nonumber \]
Applying the initial conditions, \(10(0)=0\) and \(10′(0)=−5\), we get
\[x(t)=−5e^{−2t}+5e^{−3t}. \nonumber \]
After 10 sec the mass is at position
\[x(x)=−5e^{−20}+5e^{−30}≈−1.0305×10^{−eight}≈0, \nonumber \]
so it is, effectively, at the equilibrium position. We accept \(x′(t)=10e^{−2t}−15e^{−3t}\), and so after x sec the mass is moving at a velocity of
\[x′(ten)=10e^{−xx}−15e^{−thirty}≈2.061×x^{−8}≈0. \nonumber \]
Later on only 10 sec, the mass is barely moving.
A two-kg mass is attached to a spring with spring constant 24 N/m. The organisation is then immersed in a medium imparting a damping force equal to 16 times the instantaneous velocity of the mass. Find the equation of movement if information technology is released from rest at a betoken 40 cm below equilibrium.
- Hint
-
Follow the process from the previous example.
- Reply
-
\(x(t)=0.6e^{−2t}−0.2e^{−6t}\)
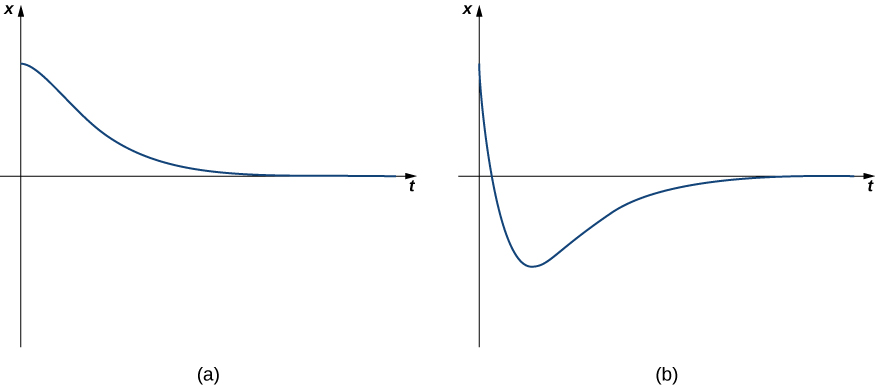
Case two: Critically Damped Vibrations
When \(b^two=4mk\), nosotros say the organisation is critically damped. The general solution has the form
\[x(t)=c_1e^{λ_1t}+c_2te^{λ_1t}, \nonumber \]
where \(λ_1\) is less than zero. The motion of a critically damped system is very similar to that of an overdamped system. It does not oscillate. However, with a critically damped system, if the damping is reduced even a little, oscillatory behavior results. From a practical perspective, physical systems are most always either overdamped or underdamped (case iii, which we consider side by side). It is impossible to fine-melody the characteristics of a physical organization so that \(b^2\) and \(4mk\) are exactly equal. Figure \(\PageIndex{6}\) shows what typical critically damped behavior looks like.
A ane-kg mass stretches a jump xx cm. The system is attached to a dashpot that imparts a damping force equal to 14 times the instantaneous velocity of the mass. Find the equation of motion if the mass is released from equilibrium with an upward velocity of three m/sec.
Solution
Nosotros have \(mg=1(9.8)=0.2k\), so \(k=49.\) And so, the differential equation is
\[x″+14x′+49x=0, \nonumber \]
which has general solution
\[x(t)=c_1e^{−7t}+c_2te^{−7t}. \nonumber \]
Applying the initial weather \(x(0)=0\) and \(x′(0)=−3\) gives
\[x(t)=−3te^{−7t}. \nonumber \]
A 1-lb weight stretches a spring half dozen in., and the organisation is fastened to a dashpot that imparts a damping forcefulness equal to half the instantaneous velocity of the mass. Find the equation of motion if the mass is released from rest at a point 6 in. beneath equilibrium.
- Hint
-
Commencement find the spring constant.
- Answer
-
\(x(t)=\dfrac{1}{2}due east^{−8t}+4te^{−8t} \)
Case 3: Undamped Vibrations
When \(b^ii<4mk\), we say the system is underdamped. The general solution has the form
\[x(t)=e^{αt}(c_1 \cos (βt) + c_2 \sin (βt)), \nonumber \]
where \(α\) is less than zero. Underdamped systems do oscillate because of the sine and cosine terms in the solution. Withal, the exponential term dominates eventually, so the amplitude of the oscillations decreases over time. Figure \(\PageIndex{vii}\) shows what typical underdamped behavior looks similar.
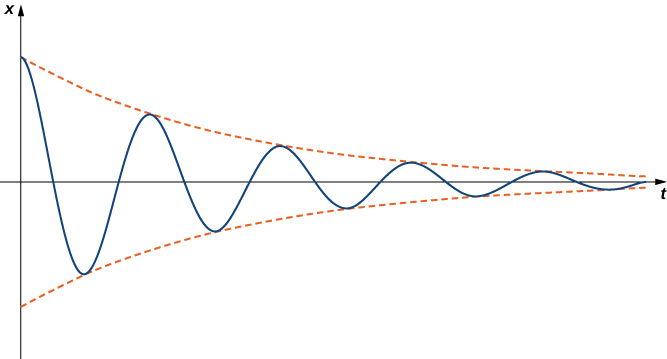
Note that for all damped systems, \( \lim \limits_{t \to \infty} ten(t)=0\). The arrangement always approaches the equilibrium position over time.
A 16-lb weight stretches a spring iii.2 ft. Assume the damping force on the system is equal to the instantaneous velocity of the mass. Observe the equation of motion if the mass is released from rest at a point 9 in. below equilibrium.
Solution
We have \(k=\dfrac{xvi}{3.2}=v\) and \(m=\dfrac{xvi}{32}=\dfrac{ane}{two},\) then the differential equation is
\[\dfrac{1}{2} 10″+10′+5x=0, \; \text{or} \; x″+2x′+10x=0. \nonumber \]
This equation has the general solution
\[x(t)=e^{−t} ( c_1 \cos (3t)+c_2 \sin (3t) ) . \nonumber \]
Applying the initial conditions, \(ten(0)=\dfrac{3}{iv}\) and \(x′(0)=0,\) we get
\[x(t)=eastward^{−t} \bigg( \dfrac{3}{iv} \cos (3t)+ \dfrac{1}{4} \sin (3t) \bigg) . \nonumber \]
A 1-kg mass stretches a bound 49 cm. The system is immersed in a medium that imparts a damping force equal to iv times the instantaneous velocity of the mass. Find the equation of motion if the mass is released from residue at a point 24 cm above equilibrium.
- Hint
-
First find the jump abiding.
- Answer
-
\(10(t)=−0.24e^{−2t} \cos (4t)−0.12e^{−2t} \sin (4t) \)
For motocross riders, the suspension systems on their motorcycles are very of import. The off-road courses on which they ride often include jumps, and losing control of the motorcycle when they state could price them the race.

This suspension arrangement can exist modeled every bit a damped jump-mass system. We define our frame of reference with respect to the frame of the motorbike. Presume the end of the shock cushion fastened to the motorbike frame is stock-still. And so, the "mass" in our spring-mass system is the motorcycle wheel. Nosotros measure out the position of the wheel with respect to the motorcycle frame. This may seem counterintuitive, since, in many cases, it is actually the motorbike frame that moves, but this frame of reference preserves the development of the differential equation that was done before. As with before development, we ascertain the downwards direction to be positive.
When the motorcycle is lifted past its frame, the wheel hangs freely and the jump is uncompressed. This is the leap's natural position. When the motorbike is placed on the footing and the rider mounts the motorcycle, the leap compresses and the organisation is in the equilibrium position (Figure \(\PageIndex{nine}\)).
This system can be modeled using the same differential equation we used before:
\[mx″+bx′+kx=0. \nonumber \]
A motocross motorcycle weighs 204 lb, and we assume a passenger weight of 180 lb. When the passenger mounts the motorcycle, the pause compresses 4 in., and so comes to rest at equilibrium. The suspension system provides damping equal to 240 times the instantaneous vertical velocity of the motorbike (and rider).
- Set up the differential equation that models the behavior of the motorcycle suspension system.
- We are interested in what happens when the motorcycle lands after taking a jump. Let fourth dimension \[t=0 \nonumber \] denote the fourth dimension when the motorcycle get-go contacts the basis. If the motorcycle hits the ground with a velocity of ten ft/sec downward, find the equation of motion of the motorcycle afterward the bound.
- Graph the equation of move over the beginning second afterwards the motorbike hits the ground.
Solution
- Nosotros have defined equilibrium to exist the point where \(mg=ks\), and then we have
\[\begin{align*} mg &=ks \\ 384 &=k\left(\dfrac{i}{3}\right)\\ k &=1152. \end{align*}\]
Nosotros as well accept
\[\brainstorm{align*} W &=mg \\ 384 &=m(32) \\ grand &=12. \end{align*}\]
Therefore, the differential equation that models the behavior of the motorcycle suspension is
\[12x″+240x′+1152x=0. \nonumber \]
Dividing through by 12, we get
\[x''+20x′+96x=0. \nonumber \]
- The differential equation institute in function a. has the general solution
\[x(t)=c_1e^{−8t}+c_2e^{−12t}. \nonumber \]
At present, to determine our initial weather condition, we consider the position and velocity of the motorbike wheel when the wheel beginning contacts the basis. Since the motorcycle was in the air prior to contacting the ground, the wheel was hanging freely and the bound was uncompressed. Therefore the wheel is 4 in. \(\left(\dfrac{1}{iii}\text{ ft}\correct)\) below the equilibrium position (with respect to the motorcycle frame), and nosotros have \(x(0)=\dfrac{one}{3}.\) According to the problem statement, the motorbike has a velocity of x ft/sec downwardly when the motorcycle contacts the basis, so \(x′(0)=x.\) Applying these initial conditions, nosotros go \(c_1=\dfrac{vii}{2}\) and \(c_2=−\left(\dfrac{xix}{vi}\right)\),so the equation of motion is
\[x(t)=\dfrac{7}{ii}eastward^{−8t}−\dfrac{19}{vi}e^{−12t}. \nonumber \]
- The graph is shown in Figure \(\PageIndex{10}\).
NASA is planning a mission to Mars. To save money, engineers take decided to adapt one of the moon landing vehicles for the new mission. Even so, they are concerned nigh how the different gravitational forces volition affect the suspension system that cushions the craft when it touches down. The acceleration resulting from gravity on the moon is 1.half-dozen yard/sec2, whereas on Mars it is iii.7 thousand/secii.
The pause system on the craft can be modeled as a damped leap-mass system. In this case, the leap is beneath the moon lander, and then the jump is slightly compressed at equilibrium, as shown in Effigy \(\PageIndex{eleven}\).
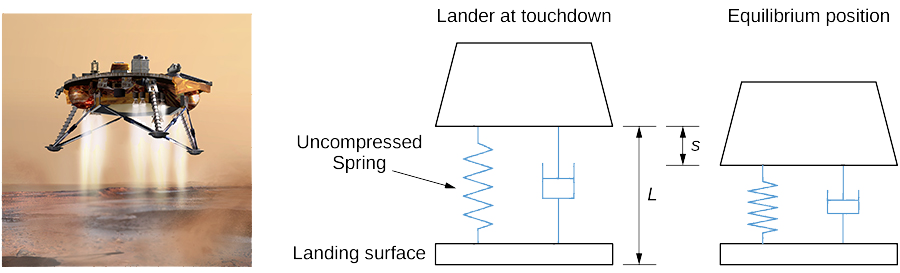
We retain the convention that downwardly is positive. Despite the new orientation, an examination of the forces affecting the lander shows that the same differential equation tin be used to model the position of the landing craft relative to equilibrium:
\[mx''+bx′+kx=0, \nonumber \]
where \(m\) is the mass of the lander, \(b\) is the damping coefficient, and \(m\) is the spring constant.
- The lander has a mass of fifteen,000 kg and the bound is ii g long when uncompressed. The lander is designed to compress the spring 0.5 m to attain the equilibrium position under lunar gravity. The dashpot imparts a damping force equal to 48,000 times the instantaneous velocity of the lander. Set up the differential equation that models the move of the lander when the arts and crafts lands on the moon.
- Let time \(t=0\) denote the instant the lander touches down. The rate of descent of the lander can exist controlled by the crew, then that it is descending at a charge per unit of 2 m/sec when it touches down. Observe the equation of move of the lander on the moon.
- If the lander is traveling too fast when it touches downwardly, information technology could fully shrink the spring and "lesser out." Bottoming out could damage the landing arts and crafts and must be avoided at all costs. Graph the equation of motility found in part two. If the spring is 0.5 g long when fully compressed, volition the lander be in danger of bottoming out?
- Assuming NASA engineers make no adjustments to the spring or the damper, how far does the lander compress the jump to achieve the equilibrium position nether Martian gravity?
- If the lander coiffure uses the same procedures on Mars as on the moon, and keeps the charge per unit of descent to two grand/sec, will the lander bottom out when it lands on Mars?
- What adjustments, if any, should the NASA engineers make to utilize the lander safely on Mars?
Forced Vibrations
The concluding case we consider is when an external force acts on the system. In the case of the motorbike suspension system, for instance, the bumps in the route act as an external force acting on the system. Another example is a spring hanging from a support; if the back up is set in motion, that move would be considered an external force on the arrangement. We model these forced systems with the nonhomogeneous differential equation
\[mx″+bx′+kx=f(t), \nonumber \]
where the external force is represented past the \(f(t)\) term. Equally we saw in Nonhomogenous Linear Equations, differential equations such as this accept solutions of the class
\[x(t)=c_1x_1(t)+c_2x_2(t)+x_p(t), \nonumber \]
where \(c_1x_1(t)+c_2x_2(t)\) is the full general solution to the complementary equation and \(x_p(t)\) is a particular solution to the nonhomogeneous equation. If the organisation is damped, \(\lim \limits_{t \to \infty} c_1x_1(t)+c_2x_2(t)=0.\) Since these terms do not affect the long-term beliefs of the system, nosotros call this part of the solution the transient solution . The long-term behavior of the arrangement is determined by \(x_p(t)\), then we call this part of the solution the steady-country solution.
A mass of one slug stretches a bound 2 ft and comes to rest at equilibrium. The system is attached to a dashpot that imparts a damping force equal to eight times the instantaneous velocity of the mass. Find the equation of motion if an external force equal to \(f(t)=8 \sin (4t)\) is applied to the organisation beginning at time \(t=0\). What is the transient solution? What is the steady-country solution?
Solution
We have \(mg=1(32)=2k,\) so \(m=16\) and the differential equation is
\[x″+8x′+16x=8 \sin (4t). \nonumber \]
The full general solution to the complementary equation is
\[c_1e^{−4t}+c_2te^{−4t}. \nonumber \]
Assuming a detail solution of the grade \(x_p(t)=A \cos (4t)+ B \sin (4t)\) and using the method of undetermined coefficients, we find \(x_p (t)=−\dfrac{1}{4} \cos (4t)\), so
\[x(t)=c_1e^{−4t}+c_2te^{−4t}−\dfrac{1}{four} \cos (4t). \nonumber \]
At \(t=0,\) the mass is at residual in the equilibrium position, so \(x(0)=x′(0)=0.\) Applying these initial conditions to solve for \(c_1\) and \(c_2,\) we become
\[x(t)=\dfrac{1}{4}e^{−4t}+te^{−4t}−\dfrac{ane}{four} \cos (4t). \nonumber \]
The transient solution is \(\dfrac{1}{iv}east^{−4t}+te^{−4t}\). The steady-state solution is \(−\dfrac{i}{4} \cos (4t).\)
A mass of 2 kg is fastened to a spring with abiding 32 N/m and comes to rest in the equilibrium position. Kickoff at time\(t=0\), an external force equal to \(f(t)=68e^{−ii}t \cos (4t) \) is applied to the system. Find the equation of motion if there is no damping. What is the transient solution? What is the steady-land solution?
- Hint
-
Find the particular solution before applying the initial conditions.
- Answer
-
\(x(t)=−\dfrac{one}{ii} \cos (4t)+ \dfrac{9}{4} \sin (4t)+ \dfrac{1}{2} e^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)
\(\text{Transient solution:} \dfrac{1}{two}eastward^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)
\(\text{Steady-state solution:} −\dfrac{1}{ii} \cos (4t)+ \dfrac{9}{4} \sin (4t) \)
Consider an undamped system exhibiting simple harmonic motion. In the existent world, we never truly have an undamped system; –some damping ever occurs. For theoretical purposes, however, we could imagine a spring-mass arrangement independent in a vacuum sleeping accommodation. With no air resistance, the mass would go along to move upwardly and down indefinitely.
The frequency of the resulting motion, given past \(f=\dfrac{one}{T}=\dfrac{ω}{2π}\), is called the natural frequency of the system. If an external force acting on the arrangement has a frequency close to the natural frequency of the system, a phenomenon called resonance results. The external force reinforces and amplifies the natural motility of the system.
- Consider the differential equation \(x″+x=0.\) Find the general solution. What is the natural frequency of the system?
- Now suppose this system is subjected to an external force given by \(f(t)=5 \cos t.\) Solve the initial-value problem \(x″+ten=5 \cos t\), \(x(0)=0\), \(x′(0)=1\).
- Graph the solution. What happens to the behavior of the system over time?
- In the existent globe, at that place is always some damping. Still, if the damping strength is weak, and the external force is strong enough, existent-globe systems can nonetheless exhibit resonance. One of the well-nigh famous examples of resonance is the plummet of the Tacoma Narrows Bridge on November vii, 1940. The bridge had exhibited strange beliefs ever since information technology was congenital. The roadway had a foreign "bounce" to it. On the day it complanate, a strong windstorm caused the roadway to twist and ripple violently. The bridge was unable to withstand these forces and it ultimately collapsed. Experts believe the windstorm exerted forces on the span that were very close to its natural frequency, and the resulting resonance ultimately shook the bridge apart.
This website contains more information well-nigh the collapse of the Tacoma Narrows Bridge.
During the short time the Tacoma Narrows Bridge stood, it became quite a tourist allure. Several people were on site the twenty-four hour period the bridge complanate, and ane of them defenseless the collapse on film.
Watch the video to see the collapse of the Tacoma Narrows Bridge "Gallopin' Gertie". https://world wide web.youtube.com/scout?5=j-zczJXSxnw
- Another real-world example of resonance is a vocaliser shattering a crystal wineglass when she sings just the right note. When someone taps a crystal wineglass or wets a finger and runs information technology around the rim, a tone can be heard. That note is created by the wineglass vibrating at its natural frequency. If a vocalizer then sings that aforementioned notation at a high enough volume, the drinking glass shatters as a result of resonance.
The Goggle box bear witness Mythbusters aired an episode on this phenomenon. Visit this website to learn more about it. Adam Brutal too described the experience. Lookout this video for his account.
The RLC Series Circuit
Consider an electrical excursion containing a resistor, an inductor, and a capacitor, as shown in Figure \(\PageIndex{12}\). Such a circuit is chosen an RLC series excursion. RLC circuits are used in many electronic systems, nigh notably as tuners in AM/FM radios. The tuning knob varies the capacitance of the capacitor, which in plough tunes the radio. Such circuits tin can be modeled by second-order, constant-coefficient differential equations.
Let \(I(t)\) announce the current in the RLC circuit and \(q(t)\) denote the charge on the capacitor. Furthermore, let \(50\) denote inductance in henrys (H), \(R\) denote resistance in ohms \((Ω)\), and \(C\) announce capacitance in farads (F). Concluding, let \(E(t)\) denote electric potential in volts (V).
Kirchhoff'south voltage dominion states that the sum of the voltage drops effectually any closed loop must exist naught. So, we demand to consider the voltage drops across the inductor (denoted \(E_L\)), the resistor (denoted \(E_R\)), and the capacitor (denoted \(E_C\)). Because the RLC circuit shown in Figure \(\PageIndex{12}\) includes a voltage source, \(E(t)\), which adds voltage to the circuit, we have \(E_L+E_R+E_C=Eastward(t)\).
We present the formulas beneath without farther development and those of you interested in the derivation of these formulas can review the links. Using Faraday's law and Lenz's law, the voltage driblet across an inductor can be shown to be proportional to the instantaneous rate of change of electric current, with proportionality constant \(L.\) Thus,
\[E_L=L\dfrac{dI}{dt}. \nonumber \]
Next, according to Ohm's law, the voltage drop across a resistor is proportional to the current passing through the resistor, with proportionality constant \(R.\) Therefore,
\[E_R=RI. \nonumber \]
Final, the voltage drop across a capacitor is proportional to the charge, \(q,\) on the capacitor, with proportionality constant \(1/C\). Thus,
\[E_C=\dfrac{1}{C}q. \nonumber \]
Calculation these terms together, we become
\[L\dfrac{dI}{dt}+RI+\dfrac{one}{C}q=Eastward(t). \nonumber \]
Noting that \(I=(dq)/(dt)\), this becomes
\[L\dfrac{d^2q}{dt^ii}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=East(t). \nonumber \]
Mathematically, this system is coordinating to the spring-mass systems nosotros have been examining in this department.
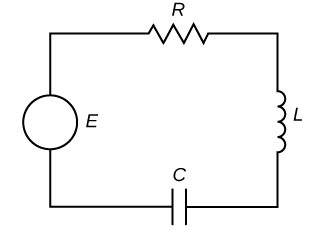
Find the charge on the capacitor in an RLC series circuit where \(Fifty=v/3\) H, \(R=10Ω\), \(C=1/30\) F, and \(Due east(t)=300\) Five. Presume the initial charge on the capacitor is 0 C and the initial current is 9 A. What happens to the charge on the capacitor over time?
Solution
Nosotros have
\[\begin{align*} L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q &=Eastward(t) \\[4pt] \dfrac{5}{3} \dfrac{d^2q}{dt^2}+x\dfrac{dq}{dt}+30q &=300 \\[4pt] \dfrac{d^2q}{dt^2}+six\dfrac{dq}{dt}+18q &=180. \end{marshal*}\]
The general solution to the complementary equation is
\[due east^{−3t}(c_1 \cos (3t)+c_2 \sin (3t)). \nonumber \]
Assume a particular solution of the form \(q_p=A\), where \(A\) is a abiding. Using the method of undetermined coefficients, nosotros discover \(A=10\). And so,
\[q(t)=due east^{−3t}(c_1 \cos (3t)+c_2 \sin (3t))+x. \nonumber \]
Applying the initial conditions \(q(0)=0\) and \(i(0)=((dq)/(dt))(0)=nine,\) nosotros find \(c_1=−10\) and \(c_2=−7.\) So the accuse on the capacitor is
\[q(t)=−10e^{−3t} \cos (3t)−7e^{−3t} \sin (3t)+10. \nonumber \]
Looking closely at this function, nosotros see the start ii terms volition decay over time (as a result of the negative exponent in the exponential function). Therefore, the capacitor eventually approaches a steady-state accuse of x C.
Detect the charge on the capacitor in an RLC series circuit where \(50=1/5\) H, \(R=2/5Ω,\) \(C=ane/ii\) F, and \(E(t)=50\) V. Assume the initial accuse on the capacitor is 0 C and the initial current is 4 A.
- Hint
-
Remember, \(E_L=L((dI)/(dt)).\)
- Answer
-
\[q(t)=−25e^{−t} \cos (3t)−7e^{−t} \sin (3t)+25 \nonumber \]
Key Concepts
- 2nd-society constant-coefficient differential equations can be used to model spring-mass systems.
- An examination of the forces on a jump-mass system results in a differential equation of the course \[mx″+bx′+kx=f(t), \nonumber \] where mm represents the mass, bb is the coefficient of the damping forcefulness, \(k\) is the spring abiding, and \(f(t)\) represents any net external forces on the system.
- If \(b=0\), in that location is no damping force interim on the organisation, and simple harmonic motion results.
- If \(b≠0\),the behavior of the system depends on whether \(b^2−4mk>0, b^2−4mk=0,\) or \(b^ii−4mk<0.\)
- If \(b^ii−4mk>0,\) the system is overdamped and does not exhibit oscillatory beliefs.
- If \(b^2−4mk=0,\) the system is critically damped. Information technology does not exhibit oscillatory behavior, but any slight reduction in the damping would issue in oscillatory behavior.
- If \(b^2−4mk<0\), the organization is underdamped. It exhibits oscillatory behavior, but the aamplitude of the oscillations decreases over time.
- If\(f(t)≠0\), the solution to the differential equation is the sum of a transient solution and a steady-land solution. The steady-state solution governs the long-term behavior of the arrangement.
- The charge on the capacitor in an RLC serial circuit can also be modeled with a second-order constant-coefficient differential equation of the class \[Fifty\dfrac{d^2q}{dt^ii}+R\dfrac{dq}{dt}+\dfrac{one}{C}q=East(t), \nonumber \] where \(L\) is the inductance, \(R\) is the resistance, \(C\) is the capacitance, and \(E(t)\) is the voltage source.
Cardinal Equations
- Equation of simple harmonic motion \[ten″+ω^2x=0 \nonumber \]
- Solution for simple harmonic motion \[ten(t)=c_1 \cos (ωt)+c_2 \sin (ωt) \nonumber \]
- Alternative form of solution for SHM \[x(t)=A \sin (ωt+ϕ) \nonumber \]
- Forced harmonic motion \[mx″+bx′+kx=f(t)\nonumber \]
- Charge in a RLC series excursion \[50\dfrac{d^2q}{dt^two}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=East(t),\nonumber \]
Glossary
- RLC series circuit
- a complete electric path consisting of a resistor, an inductor, and a capacitor; a second-order, constant-coefficient differential equation can be used to model the charge on the capacitor in an RLC series excursion
- simple harmonic motion
- motion described by the equation \(x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\), as exhibited by an undamped spring-mass system in which the mass continues to oscillate indefinitely
- steady-state solution
- a solution to a nonhomogeneous differential equation related to the forcing function; in the long term, the solution approaches the steady-country solution
Differential Equation Spring Mass System,
Source: https://math.libretexts.org/Bookshelves/Calculus/Book:_Calculus_%28OpenStax%29/17:_Second-Order_Differential_Equations/17.03:_Applications_of_Second-Order_Differential_Equations
Posted by: joynerandutimmose.blogspot.com


0 Response to "Differential Equation Spring Mass System"
Post a Comment